1. Home
2. HSC
3. HSC Exams
4. 2011 HSC Exam papers
5. 2011 HSC Notes from the Marking Centre — General Mathematics

2011 HSC Notes from the Marking Centre – General Mathematics

Contents

• Introduction
• Section II
  • Question 23
  • Question 24
  • Question 25
  • Question 26
  • Question 27
  • Question 28

Introduction

This document has been produced for the teachers and candidates of the Stage 6 General Mathematics course. It contains comments on candidate responses to the 2011 Higher School Certificate examination, indicating the quality of the responses and highlighting their relative strengths and weaknesses.

This document should be read along with the relevant syllabus, the 2011 Higher School Certificate examination, the marking guidelines and other support documents developed by the Board of Studies to assist in the teaching and learning of General Mathematics.

General comments

The instructions at the beginning of Section II indicate that all necessary working should be shown in every question. Candidates are reminded that where a question is worth several marks, full marks may not be awarded for an answer, even if the answer given is correct, if no working is shown.

Where candidates give an incorrect answer with little or no working shown, no marks can be given since markers have no indication of the candidate’s reasoning behind the solution. Candidates are advised to show all their working so that part marks can be awarded for some correct steps towards their answer. A simple example is when candidates have to round their answer to a certain degree of accuracy. Candidates should always write their calculator display before rounding their answer. They should only round their answer in the last step of working, not in an earlier step. Markers can then see that candidates have rounded correctly, even if the answer is not correct.

Some questions required candidates to explain their answer and/or justify their result in words and/or by using calculations. This presented a problem for a significant number of candidates. They need to become familiar with appropriate terminology and should read their answers after writing them to ensure that the answers make sense.

Candidates need to pay attention to the number of marks allocated to each part of a question so that they know how extensive their answers should be. They should pay particular attention to the situation where a question asks them to justify with calculations or examples, and should ensure that they respond appropriately.

Candidates should bring a ruler to the examination for drawing graphs and diagrams accurately. They should also take note of diagrams where ‘NOT TO SCALE’ is indicated, since in these cases measuring lines or angles to obtain a result will not be awarded any marks.

In better responses, candidates:

• showed a clear, concise and appropriate method to solve each problem
  
• worked in a logical manner, clearly stated what they were doing, and showed all necessary working
  
• referred correctly to the formulae sheet, were familiar with it, and used it carefully where necessary
  
• drew large, clear, well-labelled diagrams and included given information as well as information calculated while doing the question
  
• did not round off too early in their calculations
  
• articulated their explanations, either with the support of calculations or in clear written form
  
• considered the reasonableness of their answers within the context of the question.

Section II

Question 23

1. Most candidates calculated a total for tax deductions. In the best responses, candidates subtracted all the tax deductions from the gross income. Most candidates who successfully calculated the taxable income went on and accurately used percentages to calculate the Medicare levy. Those candidates who did not calculate the taxable income correctly could still use percentages to calculate the Medicare levy from what they thought was the taxable income. Candidates who showed their working were able to get marks.
   
   
2. 1. In better responses, candidates did not simply count the number of sticks. Some candidates drew an extension of the table to include the fourth figure. In better responses, candidates did not add matchsticks to the middle of the diagram.
      
      
   2. A number of different strategies were employed to solve this question. In better responses, candidates used a correct rule and used a formula to calculate the number of sticks needed to complete the figure. Other candidates who did not successfully write a rule generally counted the number of sticks by adding 3 sticks until arriving at the 100th figure. Quite a number of candidates gave wrong answers without showing working out. In better responses, candidates adequately explained the relationship using words, numbers or symbols.
      
      
   3. In better responses, candidates used the rule from part (b) (ii) and applied it successfully to determine if a figure could be made from 543 sticks. Some candidates mistakenly thought that an integer answer indicated that you could form the figure. In better responses, candidates used calculations as a basis for their answer, followed by a correct conclusion.
3. Only a small percentage of candidates obtained full marks for this question. The better candidates understood the instruction to ‘use the table’ and found appropriate values for n and r.
   
   
4. 1. Most candidates could convert between the formula forms.
      
      
   2. Although the formula for the area of the ellipse was provided on the formulae sheet, many candidates did not appear to use it. In better responses, candidates remembered to halve the axes of the ellipse. They used V = Ah successfully to find the length of the prism and did not use the surface area formula or the volume of a cylinder formula. In better responses, candidates did not round off too early in their solution and maintained accuracy in their answer.

Question 24

1. 1. Many candidates answered this question correctly.
      
      
   2. In better responses, candidates understood what was meant by the word ‘dimensions’ and successfully answered the question.
      
      
   3. Most candidates correctly answered the question. In better responses, candidates successfully subtracted the widths of the walls and did not include them in the answer.
      
      
   4. In better responses, candidates understood what was meant by ‘width’ in this context and took the window space into account in their calculation.
2. 1. In better responses, candidates provided the correct answer supported by working out that was well presented.
      
      
   2. In better responses, candidates did not confuse relative frequency with either frequency or cumulative frequency. They used a calculation to find the relative frequency.
      
      
   3. Most candidates answered this question correctly.
3. 1. In better responses, candidates displayed proficiency in both trigonometry and geometry. They showed knowledge of angles with parallel lines and understood that all north-pointing lines are also parallel. They used clear diagrams with short and concise working. Some candidates considered the distance from A to C as a horizontal line, interpreted the diagram as three dimensional, and confused the terms ‘to’ and ‘from’ with regard to a bearing.
      
      
   2. In better responses, candidates used the cosine rule, substituted the correct values, and used the calculator to correctly determine the answer. These candidates also considered the reasonableness of their answer.
      
      
   3. In better responses, candidates clearly indicated what they were doing and showed the working on the diagram. They had a clear understanding of the term ‘bearing’. These responses managed to correctly find some of the angles associated in arriving at the answer.

Question 25

1. 2. In better responses, candidates gave an appropriate question, such as ‘How many mobile phones do you own?’
      
      
   3. In better responses, candidates understood the use of the term ‘stratified’.
      
      
   4. In better responses, candidates understood the terms ‘census’ and ‘population’ and gave a specific population answer, not a general one.
2. 1. This question was well answered. In better responses, candidates answered by reading the information off the graph. They answered correctly by not confusing the ‘highest percentage’ with the ‘most phones’.
      
      
   2. In better responses, candidates successfully used a calculation to justify their answer, although many candidates noted the gap between the number of students and those who owned mobile phones to justify their answer.
      
      
   3. A range of responses indicating a trend in the data was accepted. ‘As the year group increases, the percentage of mobile phones increase’ and ‘As the year group increases, the number of candidates decreases’ were the common accepted answers. There were other accepted responses, such as the reverse of these statements. The better responses indicated a trend and did not merely state facts from the graph.
3. 1. This part was very well answered.
      
      
   2. In better responses, candidates stated probabilities as fractions, decimals or percentages. This part was well answered.
      
      
   3. In better responses, candidates calculated the total correctly, not forgetting to add the 10. They then went on to determine the correct percentage, rather than leaving their response as a fraction.
4. 1. This question was very well answered, with many correct answers of 71 for the outlier.
      
      
   2. In better responses, candidates understood the term ‘interquartile range’ and correctly calculated it.

Question 26

1. 1. This question was well answered by most candidates.
   3. In better responses, candidates showed a clear understanding of the question. They recognised that one spinner’s outcome was predetermined and that they should only be looking at the other spinner.
      
      
   4. In better responses, candidates were clearly familiar with the concept of financial expectation. They successfully calculated the financial expectation in this question and then subtracted the cost to arrive at a correct conclusion.
2. 1. This question was answered correctly by most candidates. In better responses, candidates stated a conclusion.
      
      
   2. In better responses, candidates used the required ‘guess-and-check’ method, showing populations below and above 18 000. In better responses, candidates understood that only whole numbers of t were needed and stated a correct and unambiguous conclusion.
3. In better responses, candidates showed calculations of various stages of this solution, including deposit and balance, total interest, and determining a monthly repayment. They worked through and combined all stages of the solution to determine the correct monthly repayment. They did not round off too early in their solution.

Question 27

1. In better responses, candidates showed a clear understanding of this type of graph and were well prepared to answer the question. They correctly added the data to complete the chart.
   
   
2. 1. In better responses, candidates clearly showed an understanding that 91º was the smaller angle separation. They followed the correct process and used 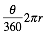 or multiplied the angle by 60NM and then by 1.852.
      
      
   2. In better responses, candidates clearly stated the degree and direction for the two values.
3. 1. This question was answered successfully by most candidates.
      
      
   2. In better responses, candidates were comprehensive in their answers, demonstrating a thorough understanding of probability and the place of z-scores in that process.
      
      For many candidates, the drawing of the normal curve was advantageous, as it showed all the percentages between the z-scores. This then allowed better candidates to rightly claim that ‘the probability of defect is 2.5% for both brands’.
4. In better responses, candidates gained full marks through using compound interest for Josephine and future value for Emma, finding the gains for each woman, and making a sensible conclusion.
   
   In better responses, candidates distinguished between loans and investments and calculated the better gain rather than the final total of the investment.

Question 28

1. 1. In better responses, candidates understood the meaning of an inverse relationship and then produced an equation linking the variables. These students managed the transition from 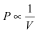 to 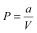 quite well. Many candidates produced linear expressions and carried this through the three parts of the question.
      
      
   2. The candidates who determined the correct expression in (a) (i) completed this section quite well and generally displayed sound equation-solving skills.
      
      
   3. In better responses, candidates had diagrams of a reasonable size, with axes well drawn and an appropriate scale. Many candidates recognised that an inverse function required a hyperbolic graph.
2. 1. In better responses, candidates determined the correct numerical value and realised that it was a negative slope.
      
      
   2. In better responses, candidates understood that the gradient was related to the depreciation of the tractor and expressed this in a clear and meaningful manner that was linked to a time period.
      
      
   3. In better responses, candidates adjusted their result from (i) to give the correct response in this part. They formed an equation containing two variables.
      
      
   4. In better responses, candidates considered n values less than zero and values greater than 15, and gave a suitable reason to justify their answer.
      
      
   5. Many candidates got full marks. They had no problem in substituting values in the formula.
      
      
   6. In better responses, candidates gave clear and unambiguous explanations that did not contain contradictory statements. They successfully stated that the salvage price would continue to decrease but would never get to zero.